🔐 Token Syndication, Economic Distribution, and Distributed Security in Polkadot

[labormedia]

Token Syndication, Economic Distribution, and Distributed Security in Polkadot

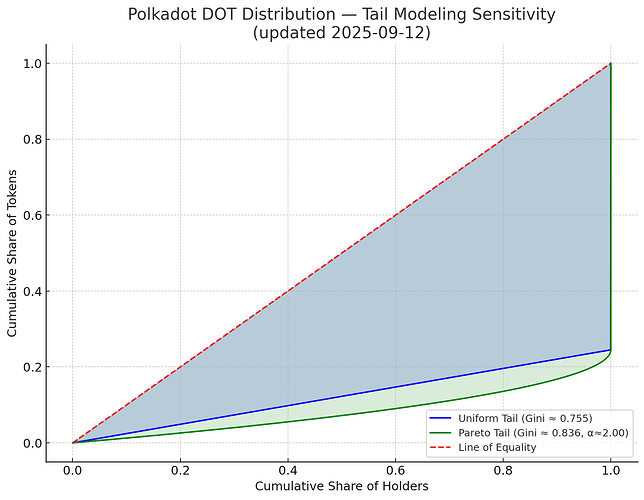
Visual Context: Gini Coefficients for DOT Token Distribution
Recent analyses estimate Polkadot’s token distribution Gini coefficient between 0.75 and 0.84, depending on whether we assume a uniform or power-law tail for small holders.
This Lorenz curve below visualizes the current state:

Blue = uniform tail (Gini ≈ 0.75), Green = Pareto tail (Gini ≈ 0.84). Top 100 holders control ~77.5% of supply.

---

1. Definitions: From Ownership to Operational Control

Let’s be precise about our terms:

• Token syndication: coordination mechanisms that route concentrated capital (large holders) into many independent operators (validators, collators, service providers) via nomination pools, delegation caps, and custody separation—without requiring redistribution.
• Economic distribution: the cash-flow spread across independent principals. What matters is not who holds tokens, but who earns revenue from protocol services.
• Distributed security: no small coalition can halt, censor, or corrupt the protocol because effective control is dispersed across uncoordinated, incentivized actors.

2. A Necessary Condition: Cost of Corruption vs. Benefit of Attack

Let:

• ( p ) = DOT price (set by market demand)
• ( S ) = total stake bonded
• ( f ) = minimum fraction of control needed to compromise the system
• ( CoC = p ⋅ S ⋅ f ) = Cost of Corruption
• ( BoA ) = Benefit of Attack (e.g., MEV, censorship, governance capture)

On any present-value basis, the system is economically secure if:

CoC > BoA

• Token syndication raises ( f ): requiring a broader coalition to attack.
• Token demand raises ( p ): increasing the cost to acquire control.

Thus, distributed security is not achieved by redistribution alone—it emerges from price × distribution of operational control.

This includes dynamic scenarios such as those discussed in previous comments of mine on threads opened by Web3 Foundation representatives discussing economic security (Polkadot’s Economic Resilience and the Role of Inflation).

3. Why Syndication Requires Economic Distribution

Syndication alone isn’t enough. If most operators are controlled by the same entity, ( f ) remains low.

To truly raise the cost of corruption:

• Delegation caps, custody diversification, and operator independence are essential.
• Cash flow must sustain those operators: decentralization is durable only if it’s economically viable.
• Economic distribution funds opex/capex without subsidies or inflation.

This keeps decentralization from becoming a short-lived grant artifact.

4. Token Demand Enforces Structural Responsibility

DOT demand does more than raise price—it enforces economic discipline:

1. Price boosts Cost of Corruption ( CoC )

Higher external demand → higher DOT price → increased ( CoC ).
Attackers must spend more capital to gain control.

2. Revenue sustains decentralization

When protocol services (e.g., coretime, identity, messaging) are priced in DOT:

• Operators earn fees.
• Independence becomes sustainable.
• Treasury dependence shrinks.

3. Performance matters under demand

Syndicated capital flows to the best operators:

• High uptime, reliability, and low latency are rewarded.
• Poor performers lose stake, flow, and relevance.
• Large holders are incentivized to optimize, not idle.

4. Demand raises the opportunity cost of collusion

Censoring or coordinating an attack costs the attacker future recurring revenue.
A high-demand protocol punishes bad actors economically.

---

4.5 Why Pricing Services in Stablecoins Reduces Economic Security

Let k ∈ [0,1] denote the demand-coupling coefficient: the fraction of service value that converts into direct DOT buy pressure (sinks/burns/bonds).

• If services are priced in DOT, k ≈ 1
• If services are priced in stablecoins, k → 0 unless the protocol forces conversion into DOT sinks

Why this weakens security:

1. Demand decoupling → Lower ( p ) and often lower ( S )
   Usage growth doesn’t require acquiring DOT. This reduces CoC = p ⋅ S ⋅ f

2. Revenue loop breaks
   Stablecoin fees bypass DOT buyback paths. Cash flow no longer supports token security.

3. Asymmetric attack calculus
   If ( BoA ) accrues in stablecoins while ( CoC ) must be paid in DOT, attack costs fall relative to benefits.

4. Operator centralization pressure
   When revenues are in stablecoins but slashing risk is in DOT, smaller operators face hedging volatility and get priced out.

Mitigations (if UX requires stablecoins):

• On-chain auto-conversion (AMM or vaults) to enforce DOT sinks . This includes my asynchronous Pareto-optimal convex optimized algorithm, but applied in this case for token exchange ( See RFC-0152: Decentralized Convex-Preference Coretime Market for Polkadot to check the setup needed for this application, with Agile Coretime as a market example and the original Paper in progress describing the algorithm construction)
• Service access bonds in DOT (collateralized metering)
• Fee burning or staking denominated in DOT

---

5. Design Rules (No Redistribution Required)

• Price services in DOT: Coretime, messaging, identity, data availability
• Syndicate with exposure caps: Encourage pool diversity and custody separation
• Pay-for-performance: Cash flows should reflect real operational value measured in service revenue
• Detect control correlation: Track and make transparent clusters among operators and entities
• Fund Treasury with KPI-bound proposals: Only back builders with DOT-denominated usage goals
• If stables are used at UX, enforce DOT sinks: Auto-convert or settle in DOT to keep ( k ) high

6. Metrics That Prove It

• Effective Nakamoto coefficient (by ultimate control, not just validator count)
• HHI or Gini of cash flows: Who earns, not who owns
• Syndication Coverage Ratio: % of stake delegated across independent operators
• Demand KPIs: DOT fees per block, coretime revenues, DOT auto-converted from stables
• Security margin: Proxy of ( CoC ) / ( BoA ) using slashing risk and market depth

---

TL;DR

• Token syndication increases ( f ), the number of actors required to attack
• Token demand increases ( p ), making DOT expensive to acquire
• Stablecoin-based service pricing decouples demand from DOT, reducing ( CoC ) unless converted into DOT sinks
• Protocol security emerges when DOT is a priced asset, not just a staked one

---

Authored by Diego Correa T.
CTIO at Ikkuna SpA · Founder | OnEdge Network
LinkedIn · GitHub

[wariomx]

gm @labormedia

I’m not an economist nor a mathematician, but your post is interesting,

Can you use the Tail model in the openGov context? (with a little switch: Tail - Active Voter Dot Distribution) How would it be?

I found a paper that makes a similar analysis on other DAOS

Today, there are approximately 140M active dots in governance, which are distributed among a few delegation accounts (DVs - W3f indirect vote), whales, W3F- direct vote, and some community DAOs, which concentrate the power in a few accounts.

In this scenario, would the value be BoA>CoC? If so, how insecure become?

Thanks in advance.

[labormedia]

gm @wariomx — excellent observation.

You’re asking the crucial question: Does the high concentration of voting power (low f) imply the governance layer is already insecure (BoA > CoC)?

Short answer: Yes, the risk is real under today’s tail dynamics. In power-law distributions, inequality within the active cohort can far exceed that of total holders. If the “Tail” (small voters) is passive, the effective f falls sharply. Your “Tail model” intuition matches the mechanics many of us worry about.

Why f mechanically drops: two scenarios

We often mistake f for a protocol constant (e.g., “51%”, “33%”). In OpenGov, the attack surface depends on the active voting set, not total stake.

Scenario A — High participation / distributed (High f)

• Thousands of independent voters participate.
• To capture a decision, an attacker must swing a broad, diverse coalition (moving along/near the line of equality).
• Result: Effective f ↑; CoC = p • S • f stays high.

Scenario B — Whale domination / low participation (Low f)

• A handful of entities dominate active voting power (deep inequality curve).
• If ~5 entities hold ≈60% of the active vote (even with a small share of total S), compromising those few is sufficient.
• Result: Effective f ↓; CoC collapses toward a simple bribe.
• Risk: Security flips if BoA outgrows this shrunken CoC.

Figure 1 — Lorenz intuition (ASCII)

Share of voters ↑
^
| 1.0 |           /  (Line of equality)
|     |          /
|     |         /
|     |        /
|     |     __/        Scenario A: mild curvature (higher f)
|     |  __/
|     | /_             Scenario B: deep tail (lower f)
|____/_/_____________________________
   0               Share of stake →             1.0

The fix: dilute politics with economics

We won’t repair a political-centralization problem by politely asking whales to participate less. We need to expand the active set from political clickers to economic producers/consumers—so influence is determined by throughput/GDP-like activity, not static balances.

This is where DAP (Allocation) and the Emergent Properties of Convex Economy / RFC-0152 (Security Coupling) naturally pair as two halves of one whole.

1) Allocation layer — DAP (stability & budgeting)

The DAP proposal inserts a buffer pool between issuance and outflows, smoothing payments and helping fund real-world expenses over time. However, this reveals a hidden variable: k.

• The Variable: k is the Cambridge Constant (inverse of Velocity, 1/V), representing the “stickiness” or demand for settlement.
• The Trap (k → 0): Price is derived from p = (GDP / S) • k. If the ecosystem routes payments purely in stablecoins without enforced DOT sinks, velocity becomes infinite and k → 0.
• The Consequence: Even if network GDP is high, if k is near zero, p crashes. Since CoC = p • S • f, security collapses.
• The Fix: DAP is only secure when inputs/output ultimately couple back to DOT (via settlement), restoring k.

2) Security layer — RFC-0152 Extended (re-coupling)

This is where the model secures the inflow and restores k. It replaces human/political pricing (auctions) with a mathematical “siphon”—a convex geometry that naturally drains value from the application layer into the settlement layer (DOT) through optimal matching.

The Mechanism: Atomic Coupling via Convex Geometry
RFC-0152 prevents users from bypassing the economic logic of the chain via a Convex Clearinghouse—a protocol-level algorithm where the only way to trade resources is to pass through a specific mathematical “gate.”

• The “Reaction” (Universal Input): Agents submit two things: a non-zero Asset Endowment (e.g., “I have 5 USDC and 0.1 Coretime”) and a Preference (α) (e.g., “I want 50% Coretime / 50% USDC”).
• The “Diffusion” (Convex Solver): The network matches buyers and sellers through a convex optimization function.
  • Influence is Bounded: All endowments secure the whole system. An agent’s influence on outputs is strictly limited to their declared initial endowments, transformations (value creation), and their preference parameter α. There is no other way to modify the outputs.
  • Stability: This conversion is atomic and deterministic. A user cannot “bribe” a validator to receive Coretime; the protocol mathematics is the exchange rate. Stability is guaranteed for the whole system if enough trading connections are met.

Figure 2 — Convex Clearinghouse (ASCII)

             (Endowments + Preference α)
[ Users / Builders ] ───────────► [ Convex Solver ] ◄────────── [ Liquidity / Peers ]
                                         │
                                         ▼
             (P2P Endogenous Atomic Swap + Forced Settlement)
                                         │
                 ┌───────────────────────┴───────────────────────┐
                 ▼                                               ▼
      [ User gets Coretime ]                           [ DOT Sink / Treasury ]

This restores CoC > BoA via two channels:

1. Diversification (f ↑): Economic activity syndicates control across many builders/operators. The effective coalition size required to corrupt grows with GDP-like activity, which is harder to monopolize than static governance stake.
2. Coupling (p ↑ via k): By forcing settlement through the convex solver, we enforce a lower bound on k.
   • Agents effectively bid up the demand for blockspace, flowing value to DOT holders/treasury.
   • They freely match their supply/demand in the market, but they operate under the strict commitment constraints defined for the model.
   • Result: k remains healthy, so as GDP grows, p grows, and Security scales with Usage.

Conclusion

Your “Tail” observation is right: when participation is thin, Scenario B risks BoA > CoC. The remedy isn’t political redistribution—it’s economic expansion with enforced coupling.

DAP stabilizes Allocation (output); RFC-0152 ensures Generation (input) clears into DOT via an endogenous, stable market. Together they lift k, support p, and broaden f, so security scales with real, decentralized usage rather than quiet coordination.